Triangle congruence proofs are an essential part of geometry, allowing students to demonstrate their understanding of the properties of triangles and how they can be proven to be congruent. These worksheets provide practice problems that help students develop their logical reasoning skills and apply the concepts they have learned in class.
By completing triangle congruence proofs worksheets, students can reinforce their knowledge of the various postulates and theorems that govern triangle congruence. These worksheets typically include a series of problems that require students to identify the given information, state the postulate or theorem that can be applied, and provide a logical argument to prove that the triangles are congruent.
One common type of problem found on triangle congruence proofs worksheets is the side-angle-side (SAS) postulate. This postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. Students must carefully analyze the information provided in each problem to determine if the SAS postulate can be applied to prove congruence.
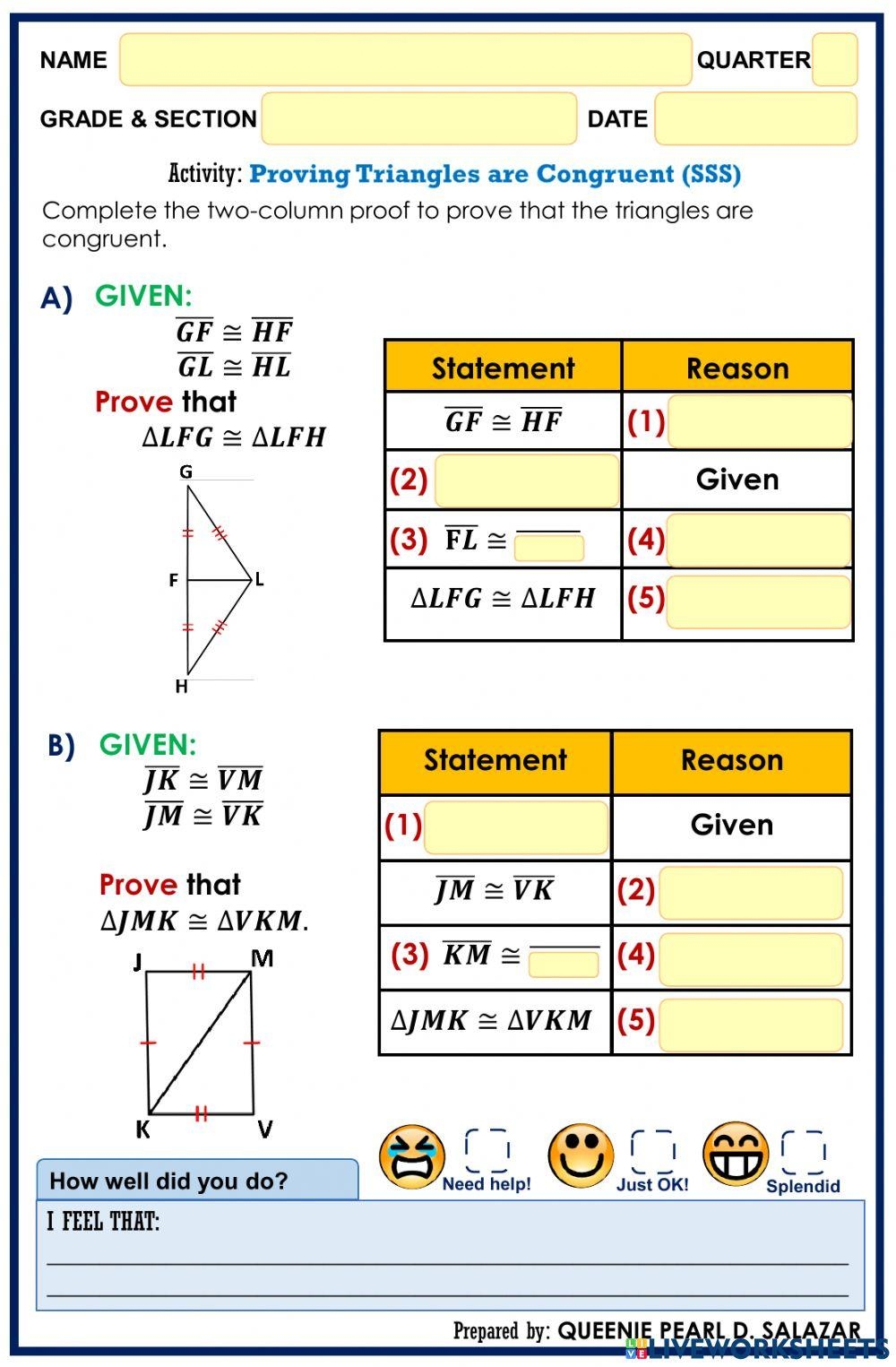
Another important postulate that students often encounter on these worksheets is the side-side-side (SSS) postulate. This postulate states that if the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent. Students must carefully measure and compare the lengths of the sides in each triangle to determine if the SSS postulate can be used to prove congruence.
Triangle congruence proofs worksheets also often include problems that require students to use the angle-side-angle (ASA) postulate or the angle-angle-side (AAS) postulate to prove congruence. These postulates state that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, or if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
In conclusion, completing triangle congruence proofs worksheets is an important part of mastering the concepts of triangle congruence in geometry. These worksheets provide students with the opportunity to practice applying postulates and theorems to prove that triangles are congruent, helping them develop their logical reasoning skills and deepen their understanding of geometric concepts.